Jarak antara titik dalam ruang berdimensi tiga merupakan materi Pelajaran Matematika kelas XII kurikulum 2013. Untuk mempelajari bagaimana menentukan jarak antara titik dalam ruang, perlu mengingat kembali teorema Phytagoras.

Teorema Pythagoras

Kenapa menggunakan teorema Pythagoras?

Teorema Pythagoras digunakan karena banyak melibatkan segi tiga siku-siku sebagai alat bantu menentukan jarak antara titik dalam ruang berdimensi tiga, baik itu jarak jarak titik dengan titik, titik dengan garis, maupun titik dengan bidang.

Pada segi tiga siku-siku, Kuadrat sisi miring sama dengan jumlah kuadrat sisi-sisi yang lainnya

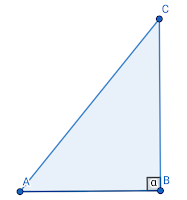
jika segitiga ABC adalah segi tiga siku-siku di mana AB sisi alas, BC sisi tegak dan AC sisi miring maka berlaku : \[{AC}^2={AB}^2+{BC}^2\]

Jarak titik dengan Titik

Jarak antara dua titik adalah lintasan terpendek antara dua titik. Perhatikan kubus ABCD.EFGH berikut ini !

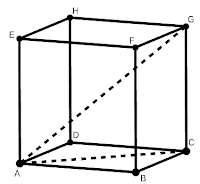
Jarak titik A ke titik G adalah panjang ruas garis A-G, bukan A-B-C-G, atau A-B-F-G. karena ruas garis A-G merupakan lintasan terpendek dari titik A ke titik G.

Garis AG juga disebut sebagai diagonal ruang kubus ABCD.EFGH. sehingga jarak titik A ke titik G sama dengan panjang diagonal ruang kubus. Jika panjang rusuk kubus adalah a, maka panjang diagonal ruang kubus tersebut adalah \(a \sqrt{3}\)

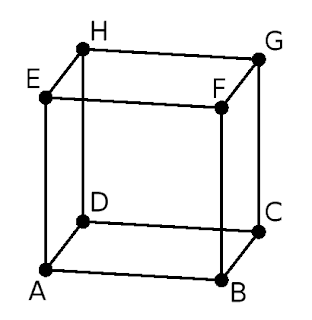
perhatikan gambar kubus dengan panjang rusuk a cm, berikut.

dari \(\Delta ACG\) diperoleh \(AG^2=AC^2+CG^2\) sehingga :

$$\begin{aligned} AG^2&=AC^2+CG^2\\ &=(AB^2+BC^2)+CG^2 \\ &=(a^2+a^2)+a^2 \\ &=3a^2 \\ AG&=\sqrt{3a^2}\\ AG&=a\sqrt{3} cm \end{aligned}$$ Jadi jarak titik A ke G adalah \(a\sqrt{3} cm \).

AC pada gambar di atas merupakan sisi miring dari segitiga ABC sehingga berdasarkan teorema pythagoras \(AC^2=AB^2+BC^2\).

selanjutnya dengan menamai panjang rusuk AG sebagai \(c\), AC sebagai \(g\) dan BG sebagai \(a\) diperoleh \(c^2=g^2+a^2\).

Contoh Soal

Dketahui sebuah Kubus ABCD.EFGH dengan panjang rusuk 4 cm. tentukan :

• jarak titik A ke B
• jarak titik A ke C
• jarak titik A ke G
• jarak titik E ke C

Penyelesaian

Diketahui pajang rusuk kubus = a = 4 cm.

• Jarak titik A ke B adalah panjang ruas garis AB = panjang rusuk AB = 4 cm
• jarak titik A ke C merupakan panjang diagonal bidang ABCD. perhatikan segitiga ABC, siku-siku di titik B, AC merupakan sisi miring \(\Delta ABC\) sehingga berlaku teorema pythagoras \(AC^2=AB^2+BC^2\). $$\begin{aligned} AC^2&=AB^2+BC^2\\ &=4^2+4^2\\ &=16+16\\ AC&=\sqrt{32}\\ AC&=\sqrt{16×2}\\ AC&=4\sqrt{2} \end{aligned}$$ jadi jarak titik A ke C adalah \(4\sqrt{2}\).
• Jarak titik A ke titik G dapat ditentukan dengan memperhatikan segitiga ACG (\(\Delta ACG\)). Pada \(\Delta ACG\) garis AG merupakan sisi miring setitiga tersebut dan sudut C adalah sudut siku-siku, sehingga berlaku teorema pythagoras : $$\begin{aligned} AG^2&=AC^2+CG^2\\ &=(4\sqrt{2})^2+4^2\\ &=16×2+16\\ &=32+16\\ AG&=\sqrt{48}\\ &=\sqrt{16×3}\\ AG&=4\sqrt{3} \end{aligned}$$ jadi jarak titik A ke titik G adalah \(4\sqrt{3}\)
• ruas garis dari titik E ke titik C merupakan diagonal ruang kubus ABCD.EFGH, sama dengan garis AG. sehingga jarak titik E ke C adalah \(4\sqrt{3}\)cm

Simpulan

• Jarak antara dua titik dalam bangun ruang merupakan lintasan terpendek yang menghubungkan kedua titik tersebut
• Untuk mementukan jarak antara dua titik yang membentuk segitiga siku-siku dapat menggunakan teorema Pythagoras
• Jarak titik yang berupa diagonal bidang kubus dapat ditentukan dengan rumus \(a\sqrt{2}\), sedangkan jarak titik yang berupa diagonal ruang kubus dapat ditentukan dengan rumus \(a\sqrt{3}\) dengan \(a\) adalah panjang rusuk kubus.