Pendahuluan
Materi Jarak titik dengan Garis ini merupakan kelanjutan dari Materi Dimensi tiga tentang Jarak Titik dengan titik dalam ruang Dimensi Tiga. Oleh karena materi ini merupakan kelanjutan dari materi sebelumnya, maka konsep jarak titik dengan titik dan penggunaan Teorema Pythagoras juga akan sering digunakan pada materi ini.
Sebagai bagian dari ilmu geometri materi ini sangat penting untuk dikuasai. Banyak aplikasi dari materi ini dalam kehidupan sehari-hari misalnya dalam membuat sebuah bangunan, penataan ruang, desain gambar tiga dimensi dan lain-lain.
Untuk memahami materi ini silahkan dicermati uraian berikut ini.
Pengertian Jarak titik ke Garis
Perhatikan Gambar berikut ini !
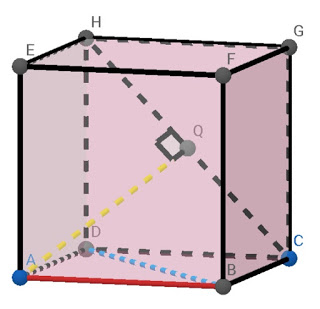
- Ruas garis AB (berwarnah merah) merupakan jarak titik A ke garis BF
- Ruas garis AQ (kuning putus-putus) merupakan jarak titik A ke garis HC
- Ruas garis BD (biru putus-putus) merupakan jarak titik B ke garis HD
Dari gambar tersebut di atas ruas nampak bahwa garis AB saling tegak lurus dengan garis BF, AQ tegak lurus dengan HC, dan BD tegak lurus dengan HD. Dari contoh-contoh tersebut dapat disimpulkan tentang pengertian jarak antar titik ke garis yaitu:
Jarak titik P ke garis k adalah: panjang ruas garis yang ditarik dari titik P tegak lurus terhadap garis k.
Untuk lebih jelasnya jarak antara titik dengan garis, perhatikan aktivitas berikut ini :
pada gambar di atas Jarak titik C ke garis f ditunjukkan oleh ruas garis CD (garis warna hijau), karena garis CD tegak lurus terhadap garis f ($\beta =90^0$).
Contoh dan Pembahasan
Contoh 1
Sebuah kubus ABCD.EFGH dengan panjang rusuk 12 cm. Tentukan jarak :
- titik A ke BC
- titik H ke AC
Pembahasan Contoh 1
Perhatikan Gambar berikut :
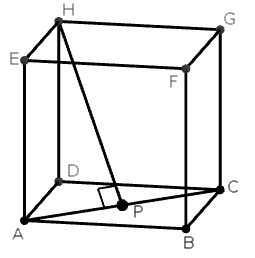
- jarak titik A ke BC = AB = 12 cm, karena AB tegak lurus garis BC
- jarak titik H ke AC adalah panjang ruas garis yang ditarik tegak lurus terhadap garis AC yaitu HP, di mana :
\begin{aligned}
HP^2&=DP^2+DH^2\\
&=(6\sqrt{2})^2+12^2 \\
HP&=\sqrt{(36 \times 2)+144}\\
&=\sqrt{216} \\
&=6\sqrt{6}
\end{aligned}
Contoh 2
Sebuah limas segi empat memiliki alas berbentuk persegi. Apabila AB = 4 cm, BC = 4 cm, dan TB = 10 cm. Tentukan jarak titik C ke garis TE, di mana titik E adalah perpotongan diagonal alas Limas.
Pembahasan Contoh 2
Dari contoh di atas diketahui :
AB=BC= 4 cm
TB = 10 cm
Ditanya :
Jarak titik C ke garis TE.
Perhatikan Gambar berikut !
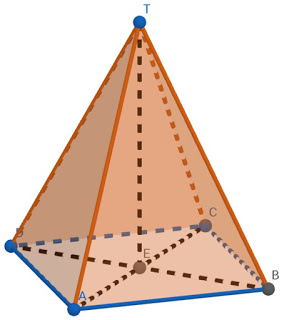
Berdasarkan gambar di atas nampak bahwa jarak titik C ke garis TE adalah panjang ruas garis CE, karena garis CE tegak lurus dengan ruas garis TE (tinggi Limas). Oleh karena panjang ruas garis CE merupakan titik tengah ruas garis AC maka panjang ruas garis CE adalah setengah dari ruas garis AC.
Selanjutnya, karena alas Limas berbetuk persegi dan ruas garis AC merupakan diagonal alas Limas, maka diperoleh panjang $AC = a\sqrt{2} $ di mana (a) adalah panjang sisi alas = 4 cm, $AC = 4 \sqrt{2} $. Sehingga diperoleh $CE=\frac {1}{2} \times 4 \sqrt{2} = 2 \sqrt{2} $.